3533

Robust Autocalibrated LORAKS for Improved EPI Ghost Correction with Structured Low-Rank Matrix Models

Rodrigo A Lobos¹, Ahsan Javed¹, Krishna S Nayak¹, W Scott Hoge^2,3, and Justin P Haldar¹

¹Electrical Engineering, University of Southern California, Los Angeles, CA, United States, ²Radiology, Brigham and Women's Hospital, Boston, MA, United States, ³Radiology, Harvard Medical School, Boston, MA, United States

Synopsis

The presence of ghost artifacts is a recurrent problem in EPI images, which has been recently addressed using structured low-rank matrix (SLM) methods. In this work we propose a new SLM ghost correction method called Robust Autocalibrated LORAKS (RAC-LORAKS). RAC-LORAKS considers autocalibrated k-space constraints (similar to GRAPPA) to deal with the ill-posedness of existing SLM EPI ghost correction methods. RAC-LORAKS additionally adapts these constraints to enable robustness to possible imperfections in the autocalibration data. We illustrate the capabilities of RAC-LORAKS in two challenging scenarios: highly accelerated EPI of the brain, and cardiac EPI with double-oblique slice orientation.

Introduction

Echo planar imaging (EPI) is prone to Nyquist ghost artifacts that appear due to mismatches between data acquired using gradients with different polarity and/or multiple shots. Conventional model-based methods¹ based on navigator information often fail in the presence of modeling errors. Recently, structured low-rank matrix (SLM) methods have been proposed to address this problem^2-5. In Ref. 5, an SLM method based on LORAKS^6,7 was introduced that incorporates autocalibrated k-space⁸ constraints (similar to GRAPPA⁹) to avoid severe ill-posedness^4,5. In this work we extend this method in order to deal with imperfections (such as ghost artifacts or phase inconsistencies) that may appear in the autocalibration data.

Theory and methods

The principle behind SLM methods is that, because k-space data is often linearly predictable (due to support, phase, parallel imaging, and sparsity constraints), it can be embedded into structured Toeplitz/Hankel matrices which will have low-rank characteristics. If the data is undersampled, then information can be recovered by applying low-rank matrix recovery to these matrices^2-8,10-12. It has been shown in earlier work^4,5 that SLM EPI ghost correction can be challenging from a theoretical perspective unless prior information is used, and that nonconvex formulations have substantial advantages over convex formulations. Reference 5 proposed a nonconvex formulation based on the LORAKS framework that incorporates prior information in the form of autocalibrated (AC) k-space constraints⁸. This “AC-LORAKS” approach was shown to be particularly powerful when compared against other approaches.

However, the good performance of the previous AC-LORAKS for EPI ghost correction relies on having high-quality autocalibration (ACS) data. This requirement is nonideal, because ACS data can often suffer from artifacts due to effects such as respiration, motion, and concomitant fields, and ACS data acquired at the beginning of a long experiment is not always consistent with EPI data measured at different timepoints. In this work, we propose a generalization of this AC-LORAKS approach called Robust Autocalibrated LORAKS (RAC-LORAKS) which is designed to be robust against ACS data imperfections. The main idea is that we do not totally trust the ACS data, and use a formulation that balances the information learned from the ACS data with information from the measured data being reconstructed. Using an alternating minimization approach, RAC-LORAKS solves the following constrained optimization problem subject to data consistency:

{\hat{k}, \hat{N}} = \arg min_{k, N} ‖ N C (k) ‖_{2}^{2} + λ_{c} ‖ N C (k_{a c s}) ‖_{2}^{2} + λ_{s} J (S (k)),

$\{\hat{\mathbf{k}},\hat{\mathbf{N}}\}=\arg\min_{\mathbf{k},\mathbf{N}}\|\mathbf{N}\mathbf{C}(\mathbf{k})\|_2^2+ \lambda_c\|\mathbf{N}\mathbf{C}(\mathbf{k_{acs}})\|_2^2+\lambda_sJ(\mathbf{S}(\mathbf{k})),$

where $\mathbf{C}(\mathbf{k})$ and $\mathbf{S}(\mathbf{k})$ are C-LORAKS (which encourages support and parallel imaging constraints) and S-LORAKS (which encourages support, parallel imaging, and phase constraints) matrices^6,7 formed from the multi-channel k-space data $\mathbf{k}$ ; $\mathbf{C}(\mathbf{k}_{acs})$ is the C-LORAKS matrix of the ACS data $\mathbf{k_{acs}}$ ; $\mathbf{N}$ is an approximate nullspace that is shared between $\mathbf{C}(\mathbf{k})$ and $\mathbf{C}(\mathbf{k}_{acs})$ ; $J$ is a nonconvex function that encourages low-rank⁸; and $\lambda_c$ and $\lambda_s$ are regularization parameters. The previous AC-LORAKS approach for EPI ghost correction⁵ can be obtained in the limit as $\lambda_c\rightarrow \infty$ , in which case the approximate nullspace $\mathbf{N}$ is a fixed matrix that is influenced only by the ACS data. The extent to which the ACS data is trusted is controlled by the value of $\lambda_c$ .

Results

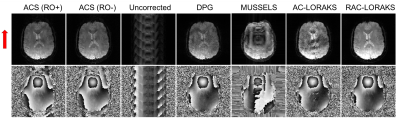
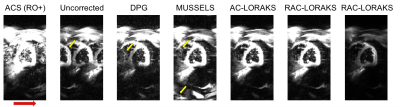
RAC-LORAKS was evaluated in the context of two challenging scenarios. In the first experiment, EPI brain data was acquired using a 32-channel receiver array and an acceleration factors of

R = 6

$R=6$ . This highly-undersampled data is very challenging to reconstruct for most constrained reconstruction methods, especially when noting that each gradient polarity has an effective acceleration factor of

R = 12

$R=12$ . In the second experiment, unaccelerated mid-short axis EPI cardiac data was acquired using a 8-channel cardiac coil and a double-oblique slice orientation¹³. This case is challenging because of the concomitant fields associated with the double-oblique orientation, as well as the time varying behavior of the heart. For both datasets, ACS data was acquired using temporal encoding (by modulating the polarity of the readout gradients¹⁴). Figures 1 and 2 show the results for the brain and cardiac data, respectively. It can be observed that RAC-LORAKS outperforms the previous AC-LORAKS method for EPI ghost correction^4,5, and other state-of-the-art methods such as dual-polarity GRAPPA (DPG)¹⁵ and MUSSELS³. RAC-LORAKS still performs well even when the ACS data demonstrates severe ghost-artifacts.

Discussion and conclusions

We proposed a new SLM method for EPI ghost-correction which uses concepts from previous LORAKS^6,7 and AC-LORAKS^4,5,8 approaches but is robust to possible imperfections in the ACS data. Our results showed that RAC-LORAKS outperforms state-of-the-art methods in two challenging scenarios, and we believe this good performance will generalize to a wide range of EPI applications. We also believe that the same kind of approach can be applied for non-EPI reconstruction problems where autocalibration data is imperfect.

Acknowledgements

This work was supported in part by research grants NSF CCF-1350563, NIH R21 EB022951, NIH R01 NS074980, and NIH R01 NS089212.

References

[1] Bernstein MA, King KF, Zhou XJ. Handbook of MRI pulse sequences. Elsevier, 2004.

[2] Lee J, Jin KH, Ye JC. "Reference-free single-pass EPI Nyquist ghost correction using annihilating filter-based low rank Hankel matrix (ALOHA)." Magnetic Resonance in Medicine, 2016.

[3] Mani M, Jacob M, Kelley D, Magnotta V. "Multi‐shot sensitivity‐encoded diffusion data recovery using structured low‐rank matrix completion (MUSSELS)." Magnetic Resonance in Medicine, 2016.

[4] Lobos RA, Kim TH, Hoge WS, Haldar JP. "Navigator-free EPI ghost correction using low-rank matrix modeling: Theoretical insights and practical improvements. " Proc. ISMRM 2017, p. 0449.

[5] Lobos RA, Kim TH, Hoge WS, Haldar JP. "Navigator-free EPI ghost correction with structured low-rank matrix models: New theory and methods. " arXiv: 1708.05095, 2017.

[6] Haldar JP. "Low-rank modeling of local-space neighborhoods (LORAKS) for constrained MRI." IEEE Transactions on Medical Imaging 33:668-681, 2014.

[7] Haldar JP, Zhuo J. "P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data." Magnetic Resonance in Medicine, 2015.

[8] Haldar JP. "Autocalibrated LORAKS for fast constrained MRI reconstruction." Proc. IEEE International Symposium on Biomedical Imaging 2015, pp. 910-913.

[9] Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. "Generalized autocalibrating partially parallel acquisitions (GRAPPA)." Magnetic Resonance in Medicine 47:1202-1210, 2002.

[10] Shin PJ, Larson PE, Ohliger MA, Elad M, Pauly JM, Vigneron DB, Lustig M. "Calibrationless parallel imaging reconstruction based on structured low‐rank matrix completion." Magnetic Resonance in Medicine 72:959-970, 2014.

[11] Jin, KH, Lee, D, Ye JC. “A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix”. IEEE Transactions on Computational Imaging, 2(4), 480-495, 2016.

[12] Ongie G, Jacob M. Off-the-grid recovery of piecewise constant images from few Fourier samples. SIAM Journal on Imaging Sciences, 9(3), 1004-1041, 2016.

[13] Javed A, Nayak KS. "Cardiac ASL using Single-Shot EPI at 3T. " Proc. ISMRM 2017, p. 3237

[14] Hoge WS, Tan H, Kraft RA. "Robust EPI Nyquist ghost elimination via spatial and temporal encoding." Magnetic Resonance in Medicine 64:1781-1791, 2010.

[15] Hoge WS, Polimeni JR. "Dual-polarity GRAPPA for simultaneous reconstruction and ghost correction of echo planar imaging data." Magnetic Resonance in Medicine, 2015.

Figures

(top) Magnitude and (bottom) phase images corresponding to the (ﬁrst two columns) ACS data and (remaining columns) image reconstruction results obtained from multi-channel EPI data prospectively undersampled by a factor or 6. Considerable ghost artifacts (which are particularly visible in the phase images) are observed in the ACS data. The red arrow indicates the phase encoding direction.

Magnitude images corresponding to the (ﬁrst column) positive gradient polarity image of the ACS data and (remaining columns) image reconstruction results obtained from unaccelerated double-oblique cardiac EPI data. In the ﬁrst six columns, the colorscale has been adjusted to highlight ghost artifacts. The last column shows a standard intensity window for reference, using the same RAC-LORAKS image as in the sixth column. The red arrow indicates the phase encoding direction. The yellow arrows are used to indicate undesired ghost artifacts.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

3533