0137
Joint estimation of arterial input function and tracer kinetic parameters from under-sampled DCE-MRI1Electrical Engineering, University of Southern California, Los Angeles, CA, United States, 2GE Healthcare, Calgary, AB, Canada
Synopsis
Direct reconstruction of tracer kinetic (TK) parameter maps from under-sampled DCE-MRI has recently been demonstrated. However, this method assumes the arterial input function (AIF) is known or pre-determined. Any mismatches between the assumed AIF and the underlying patient-specific AIF can cause large inaccuracies in the final TK parameters. We propose a novel approach to extract patient-specific AIFs from under-sampled data, while jointly estimating the TK parameter maps. Reconstruction is performed by cycling through the problems of AIF extraction, TK parameter estimation and, data consistency. We demonstrate this approach on brain tumor DCE data sets, where high fidelity AIFs are extracted up to an under-sampling rate of 100x.
Introduction
Direct Dynamic Contrast Enhanced (DCE) MRI reconstruction approaches have been proposed to estimate tracer kinetic (TK) parameter maps from under-sampled (k,t)-space data1,2,3,4. These methods have been shown to be superior to indirect reconstruction (e.g. compressed sensing followed by TK modeling). A major limitation is that such methods require a pre-determined arterial input function (AIF), often in the form of a population-averaged AIF5. Due to a combination of factors including weight-dose mismatch, unknown injection rates, cardiac/pulmonary bolus delay and dispersion, the patient-specific AIF (denoted pat-AIF) is often different from the population-averaged AIF (denoted pop-AIF), and, ignorance of such mismatch is known to cause substantial errors in TK mapping6. In this work, we demonstrate a novel approach to decouple the reconstruction problem into two sub-problems: data consistency (SENSE reconstruction) and model consistency (TK modeling including pat-AIF estimation). We show that, by this formulation, it is possible to estimate both pat-AIF and TK parameter maps directly from under-sampled data.Methods
We formulate the joint recovery of the concentration time profiles ($$$C_t$$$), patient-specific AIF (AIF), and tracer kinetic parameters ($$$\theta$$$, including $$$K^{trans}, v_p$$$ etc. depending on the model) as the following penalized optimization problem: $$(C_t, \theta, AIF )= \underset{C_t, \theta, AIF}{argmin}||AC_t-b_1||_2^2+ \beta ||P(\theta, AIF)-C_t||_2^2\quad (1)$$
where the operator A=UFS$$$\psi$$$ involves under-sampling (U), Fourier transform (F), sensitivity encoding (S) and contrast concentration to signal difference conversion ($$$\psi$$$). P represents the operation of mapping the TK parameters to contrast concentration ($$$C_t$$$), with estimation of AIF from $$$C_t$$$. P can be non-linear depending on the TK model. $$$b_1= (y+AS_0)$$$, where y is the acquired (k,t)-space data which may be sampled below the Nyquist rate, and $$$S_0$$$ is the pre-determined fully-sampled pre-contrast image. Compared to the direct reconstruction3, this approach decouples TK modelling from the data consistency, and poses TK modelling as a constraint with penalty $$$\beta$$$. This formulation allows estimation of pat-AIF from intermediate $$$C_t$$$, when we use an alternating approach as shown below for each iteration n: $$C_t^{n+1}= \underset{C_t}{argmin}||AC_t-b_1||_2^2+ \beta ||P(\theta^n, AIF^n)-C_t||_2^2\quad (2)$$ $$(\theta^{n+1}, AIF^{n+1})=P^{-1}(C_t^{n+1})\quad (3)$$ Eqn (2) is similar to a SENSE reconstruction problem that can use conjugate gradients to solve the concentration vs. time profiles ($$$C_t$$$). Eqn (3) is backward TK modelling from images including pat-AIF estimation. An arterial ROI of roughly 15 pixels is manually segmented once, using the time-averaged image. Within each iteration, we: 1) apply this ROI to $$$C_t$$$ to estimate the AIF (averaging the pixels), and 2) use the updated AIF during TK modelling. We evaluated this technique using fully-sampled DCE-MRI data sets from brain tumor patients (3T GE MRI, FOV: 22cm, spatial resolution: 0.9×1.3×7.0 mm3, 5-sec temporal resolution, 50 time frames, fast spoiled gradient echo sequence). Randomized golden-angle radial sampling pattern7 was used to retrospectively undersample data in the kx-ky plane, simulating the ky-kz plane in a 3D whole-brain acquisition8. Undersampling rates (R) from 20 to 100 were used to test the performance of proposed method. Reconstructed pat-AIF and TK maps were compared to pat-AIF and TK maps from fully-sampled data (reference) for evaluation. Only the brain part for the TK maps is stripped out after reconstruction to avoid viewing distraction.
Results
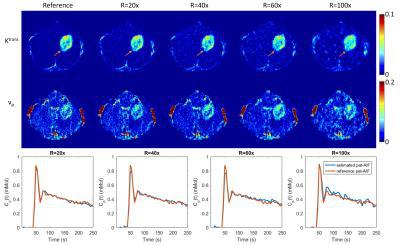
Figure 1 shows Patlak model $$$K^{trans}$$$ and $$$v_p$$$ maps (only brain part is shown) from fully-sampled data, using pop-AIF or pat-AIF. Although in this case pop-AIF is close to pat-AIF in shape, the resulting $$$K^{trans}$$$ maps are still significantly different.
Figure 2 shows the reconstructed TK parameter maps ($$$K^{trans}$$$ and $$$v_p$$$ Patlak model) for different Rs up to 100x, and the reconstructed AIF at these Rs. The proposed method is able to restore both TK maps and pat-AIF from highly under-sampled data, and mitigates the overestimation that is caused by using a pop-AIF. Adequate quality TK maps and pat-AIFs were restored at under-sampling rates up to 60x. At R=100x, the reconstructed pat-AIF showed obvious deviation from the reference, resulting in larger bias for the TK maps.
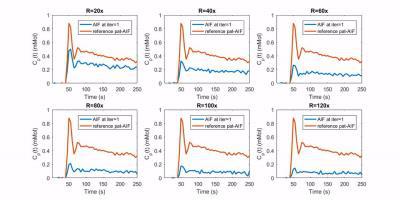
Figure 3 (gif) shows the changes in estimated pat-AIF during iterations for different undersampling rates (more Rs are shown). At lower Rs the convergence to the reference pat-AIF is faster, while at higher Rs, the proposed method is still able to restore acceptable pat-AIF after a larger iteration number.
Conclusion
We have demonstrated a novel formulation for TK model-based DCE-MRI reconstruction, where data-consistency and TK model-consistency are decoupled. This formulation is able to estimate both the patient-specific AIF and TK parameters directly from under-sampled data. Compared to using a population-based AIF, which is blind to patient-specific information, this method is able to restore high quality AIF, yielding more accurate TK parameter maps.Acknowledgements
No acknowledgement found.References
1. Dikaios N, Arridge S, Hamy V, Punwani S, Atkinson D. Direct parametric reconstruction from undersampled (k, t)-space data in dynamic contrast enhanced MRI. Med Image Anal. 2014 May24;18(7):989–1001.
2. Awate SP, DiBella EVR, Tasdizen T, Whitaker RT. Model-based image reconstruction for dynamic cardiac perfusion MRI from sparse data. IEEE-EMBS, 2006. p.936–41.
3.Guo Y, Lingala SG, Zhu Y, Lebel RM, Nayak KS. Direct Estimation of Tracer-Kinetic Parameter Maps From Highly Undersampled Brain Dynamic Contrast Enhanced MRI. MRM. 2016; (early view)
4. Guo Y, Lingala SG, Zhu Y, Lebel RM, Nayak KS. Direct Reconstruction of Kinetic Parameter Maps in Accelerated Brain DCE-MRI using the Extended-Tofts Model. ISMRM. 2016. p.0868.
5. Parker GJM, Roberts C, Macdonald A, Buonaccorsi G a, Cheung S, Buckley DL, et al. Experimentally-derived functional form for a population-averaged high-temporal-resolution arterial input function for dynamic contrast-enhanced MRI. Magn Reson Med. 2006 Nov;56(5):993–1000.
6. Port, R. E., Knopp, M. V., Brix, G. (2001). Dynamic contrast-enhanced MRI using Gd-DTPA: Interindividual variability of the arterial input function and consequences for the assessment of kinetics in tumors. MRM, 45(6), 1030–1038.
7. Zhu Y, Guo Y, Lingala SG, Marc Lebel R, Law M, Nayak KS. GOCART: GOlden-angle CArtesian randomized time-resolved 3D MRI. Magn Reson Imaging 2016;34:940–950.
8. Guo Y, Lebel RM, Zhu Y, Lingala SG, Shiroishi MS, Law M, Nayak K. High-resolution whole-brain DCE-MRI using constrained recon- struction: prospective clinical evaluation in brain tumor patients. Med Phys 2016;43:2013–2023.
Figures